Prime Numbers: One of the Most Fascinating Mathematical Mysteries
Prime numbers have been known since the dawn of time and their principle is simple to understand. And yet, their mystery continues to fascinate mathematicians for centuries.
As the magazine Québec Science jokes, "even the most powerful computers fail - or rather their circuits - on questions that were already being asked in Antiquity" according to a Google translation of author Marnie Corniou's comments about these complicated numbers.
Photo: Markus Spiske / Unsplash
"Prime numbers are one of those eternal mysteries: they have kept the greatest mathematicians in suspense," Cornious explained Let's take a look at prime numbers and the mysteries that still surround them.
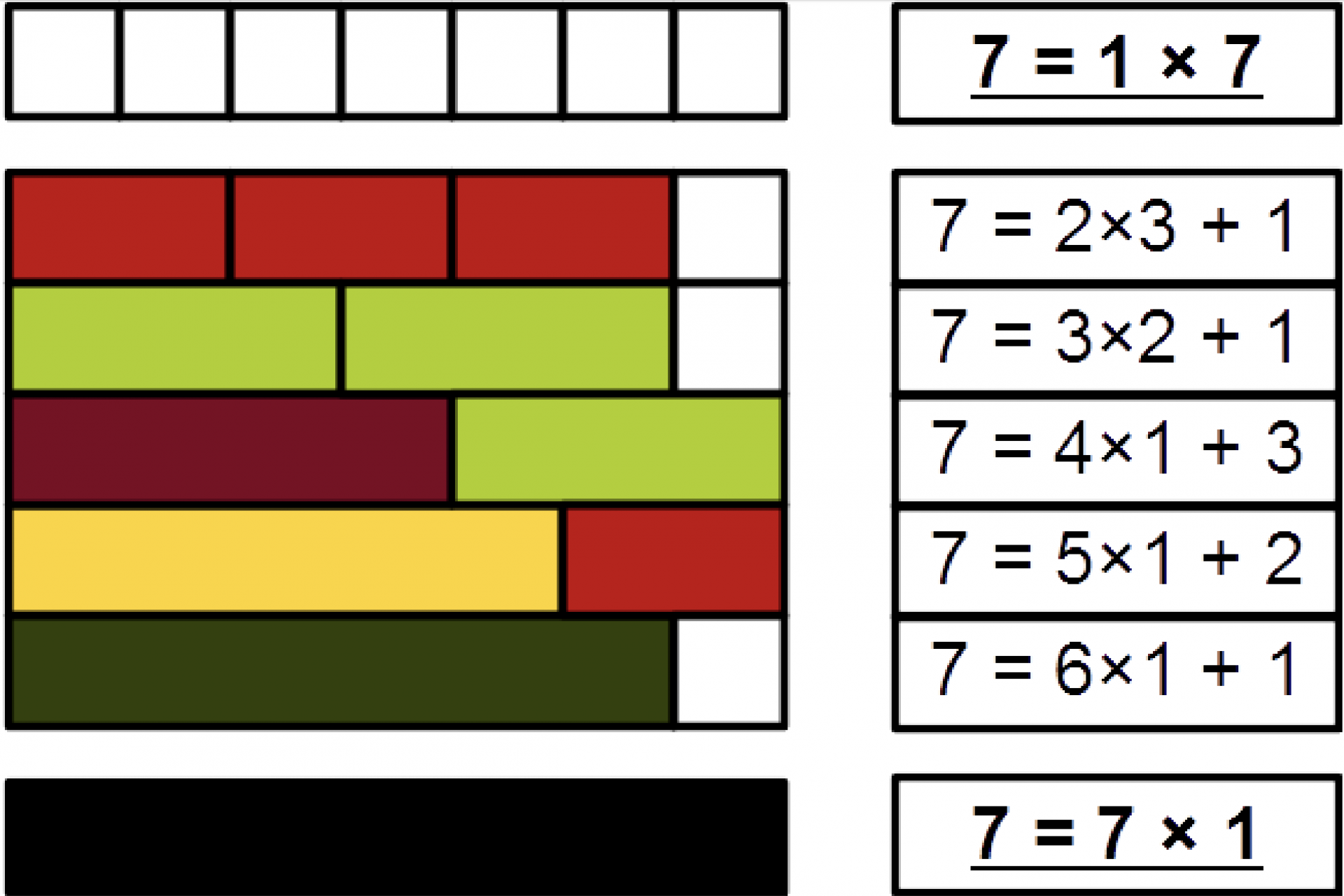
What is a prime number? These are whole numbers that are only divisible by one and by themselves. This is the case, for example, of 7, but not of 9, which can be divided into 3 x 3.
Photo: Nadine E / Unsplash
The series of prime numbers begins with very familiar numbers (2, 3, 5, 7, 11…), but it continues to infinity. No one can therefore estimate the total number of numbers or know the highest of them.
Photo: Nick Hillier / Unsplash
Andrew Granville, a specialist in number theory at the University of Montreal, quoted by Québec Science, said that prime numbers are "the fundamental bricks of mathematics, the DNA of whole numbers."
In fact, every integer can be broken down into a unique combination of prime numbers. For example, 27 is 3 x 3 x 3 and 210 is 2 x 3 x 5 x 7.
Photo: Scott Rodgerson / Unsplash
Although famous and familiar, prime numbers continue to elude any attempt to formalize their succession in the order of numbers. No simple formula can thus reveal them all.
Photo: Paul Bergmeir / Unsplash
In the 18th century, the German mathematician Christian Goldbach hypothsized that every even integer greater than two is the sum (not the product) of two prime numbers.
Photo: Adrian Curiel / Unsplash
Goldbach's conjecture hypothesis is still considered very probable by mathematicians, but it has never been proven. In any case, it is verified from 4 to 4,000,000,000,000,000,000 (4 billion billion).
The YouTube channel Science Vivante notes that there is a decrease in the frequency of prime numbers as we move away from 0: for example, there are 25 prime numbers between 0 and 100 (25% of the total), 168 between 0 and 1000 (16.8%) and 1229 between 0 and 10,000 (12.3%).
Photo: CHUTTERSNAP / Unsplash
If prime numbers are continuous and proven, something that ancient mathematician Euclid may have proven in antiquity with his now-renowned Euclid's Theorem, then there exists an infinity of prime numbers, which is a dizzying concept to think about!
Photo: Compare Fibre / Unsplash
You may have heard about prime numbers before. But do you also know about twin prime numbers? These are prime numbers that have only a difference of two, such as 5 and 7, 11 and 13, or 17 and 19. They would also be infinite and are just as increasingly rare as they move away from zero.
Photo: Anne Nygård / Unsplash
There are variations of these twins, such as cousin primes, which are four apart (like 7 and 11, or 13 and 17), and even more interesting primes, which are six apart (like 23 and 29).
Photo: Ryoji Iwata / Unsplash
In 2013, mathematician Yitang Zhang made a breakthrough in the field of prime numbers mathematics by showing that among these gaps (2, 4, 6, etc.), there was at least one, less than 70 million, for which the number of pairs of prime numbers is infinite.
Photo Credit: Wiki Commons By VOA, Public Domain
Other mathematicians have subsequently shown that this is the case at least once for a gap between 2 and 246.
In any case, the differences between prime numbers remain random, and their distribution does not obey any known rule or any apparent logic.
In the 19th century, the German mathematician Bernhard Riemann put forward the (unproven) hypothesis that nature had instead distributed these numbers as fairly as possible.
Les Echos points out that their distribution would present a resemblance to that of the "energy levels of large atomic nuclei" according to a Google translation of the outlet's comments. Enough to interest many others about prime numbers in disciplines that aren't mathematics!
Photo: Hal Gatewood / Unsplash
The proof of the Riemann hypothesis is in any case one of the seven "millennium problems" designated by the Clay Institute of Mathematics, which has promised a million dollars to anyone who can prove it. The enigma of prime numbers is still far from being solved!
By Hyacinth, Own Work, CC BY-SA 4.0
More for you
Top Stories